

Most tables go up to 30 degrees of freedom and then stop. The rows of a t-table correspond to different degrees of freedom.
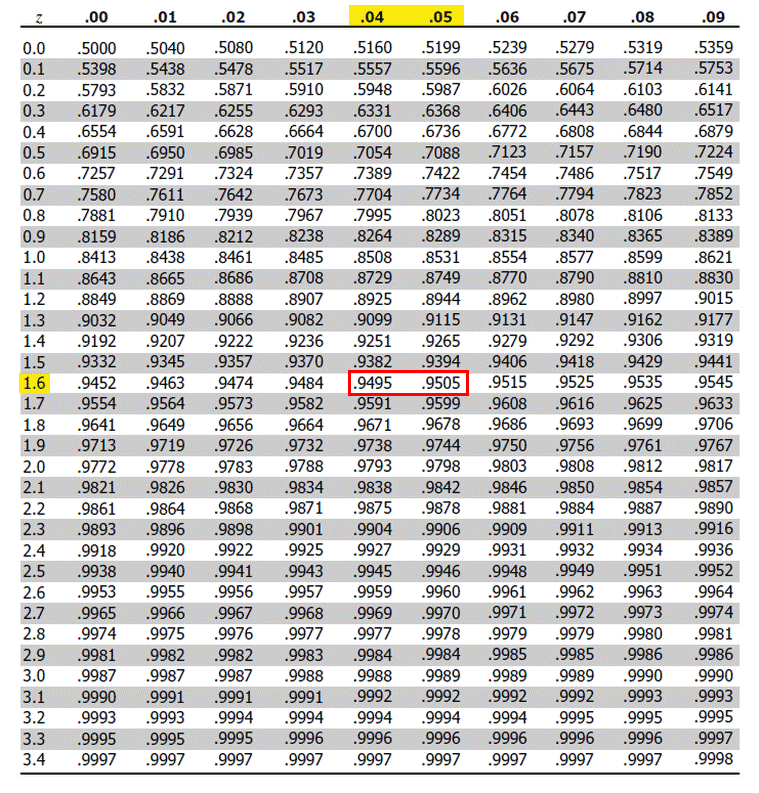
Identify if the table is for two-tailed or one-tailed tests.
#STANDARD NORMAL TABLE CRITICAL VALUE Z HOW TO#
The steps below describe how to use a typical t-table. But many statistics books still show t-tables, so understanding how to use a table might be helpful.
#STANDARD NORMAL TABLE CRITICAL VALUE Z SOFTWARE#
Most people use software to perform the calculations needed for t-tests.
This similarity is one reason why a z-distribution is used in statistical methods in place of a t-distribution when sample sizes are sufficiently large. The figure uses a dotted-line green curve for z, so that you can see both curves. Figure 2 below shows a t-distribution with 30 degrees of freedom and a z-distribution. These two distributions are very similar.Ī common rule of thumb is that for a sample size of at least 30, one can use the z-distribution in place of a t-distribution. Then compare the blue curve with 10 degrees of freedom to the green curve for the z-distribution. The t-distribution with one degree of freedom is shorter and has thicker tails than the z-distribution. Compare the pink curve with one degree of freedom to the green curve for the z-distribution. You can see how the curves with more degrees of freedom are more like a z-distribution. All three t-distributions have “heavier tails” than the z-distribution. The curves with more degrees of freedom are taller and have thinner tails. The shape of the t-distribution depends on the degrees of freedom. As the sample size increases, the t-distribution becomes more similar to a normal distribution.Ĭonsider the following graph comparing three t-distributions with a standard normal distribution:Īll of the distributions have a smooth shape.The t-distribution is most useful for small sample sizes, when the population standard deviation is not known, or both.The t-distribution is defined by the degrees of freedom.The t-distribution does not make this assumption. The normal distribution assumes that the population standard deviation is known.Like a standard normal distribution (or z-distribution), the t-distribution has a mean of zero.If you think about folding it in half at the mean, each side will be the same. Like the normal distribution, the t-distribution is symmetric.Like the normal distribution, the t-distribution has a smooth shape.Instead of diving into complex math, let’s look at the useful properties of the t-distribution and why it is important in analyses. It has a precise mathematical definition. The t-distribution is similar to a normal distribution.


 0 kommentar(er)
0 kommentar(er)
